Why Clocks Tick Differently in Space
Time may seem to be constant and universal, but under certain conditions, it can bend and warp to become unrecognisable.

It could come as a surprise to many that time passes differently depending on where you are in space. Gravitational time dilation shows that a clock on earth moves slower than a clock in outer space. I.e. time moves slower in the proximity of large masses.
In practice, clock coherence is crucial for Telemetry and Telecommand communication between the Earth and satellites. The difference in gravitational energy experienced by a clock on a satellite and on earth causes a very small difference in how the clocks run but over time it could cause miscalculations due to the clocks going out of sync. Knowledge of time dilation allows engineers to account for the discordance by choosing clocks which are appropriately slower for satellites and their orbit. GPS satellites also work because of another type of time dilation due to motion and the nature of spacetime.
Theoretical Analysis
To understand gravitational time dilation, it's essential to first grasp the theories it originates from: General Relativity and Special Relativity.
Special Relativity, in the simplest form, deals with how space interacts with time for bodies which are not accelerating, so called inertial frames of reference. It is based on just two postulates: Laws of Physics are identical in all frames of reference, the speed of light is the same for all observers. Time dilation due to movement is the first step in understanding its gravitational counterpart. In special relativity, an object moving at a speed approaching the speed of light will feel a slowing of time. In practice, this effect is negligible as objects in motion reach only a very small fraction of the speed of light.
A definition of time
The SI unit of time is a second, and the official definition of one is this: “The second is the duration of 9,192,631,770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the caesium-133 atom. This definition refers to a caesium atom at rest at a temperature of 0 Kelvin.”
The most precise instrument of measuring time is an atomic clock. An atomic clock works by counting the oscillations between two mirrors. After exactly 9,192,631,770 oscillations, a second has passed.
Suppose there are two identical atomic clocks A (left), B (right) with B being at motion relative to the stationary A.
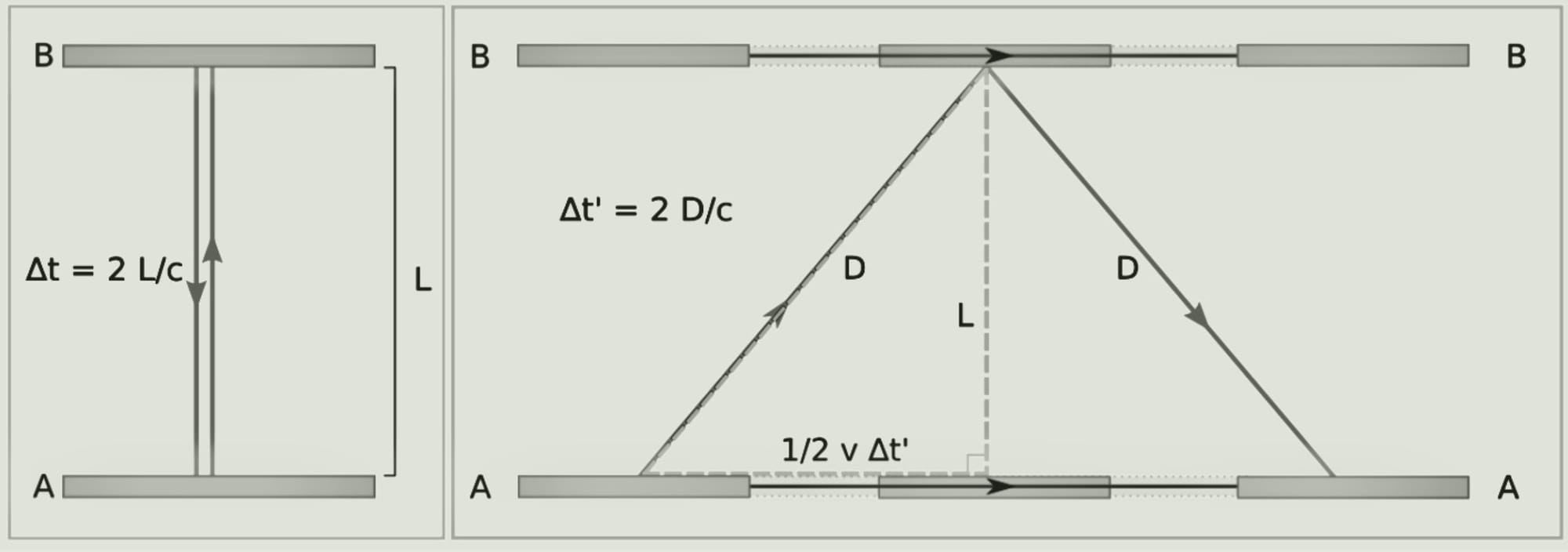
In clock A, the light only moves up and down, the shortest distance between the mirrors. This equates to the change in time being equal to exactly two times the distance between the mirrors divided by the speed of light in a vacuum. Conversely, the light ray in clock B travels across a slanted path between the mirrors when looked at by an external observer.
In clock A:
\[Δt=\frac{2L}{c}\]
In clock B:
\[Δt'=\frac{2D}{c}\]
\[D=\sqrt{\frac{vΔt'}{2}^2+ L^2}\]
Elimination of the variables D and L results in:
\[Δt'=\frac{Δt}{\sqrt{1-\frac{v^2}{c^2}}}=γΔt\]
Lorentz factor
\[γ=\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\]
Conserving the passage of time would mean that light has to speed up in clock B as it must travel a greater distance in the same amount of time however this is not possible according to the second postulate.
To an observer moving with clock B would experience clock A as slow but the same is true for one moving with clock A. In Einstein's theory of special relativity, an object can only be in motion relative to another. With no reference point, an observer travelling with clock A has no way of differentiating between a stationary clock A and a moving clock B, a moving clock A and a stationary clock B, and any combination of the two. Therefore, time in Special relativity appears to slow down in the other clock for both observers. This paradox can best be illustrated using a diagram.
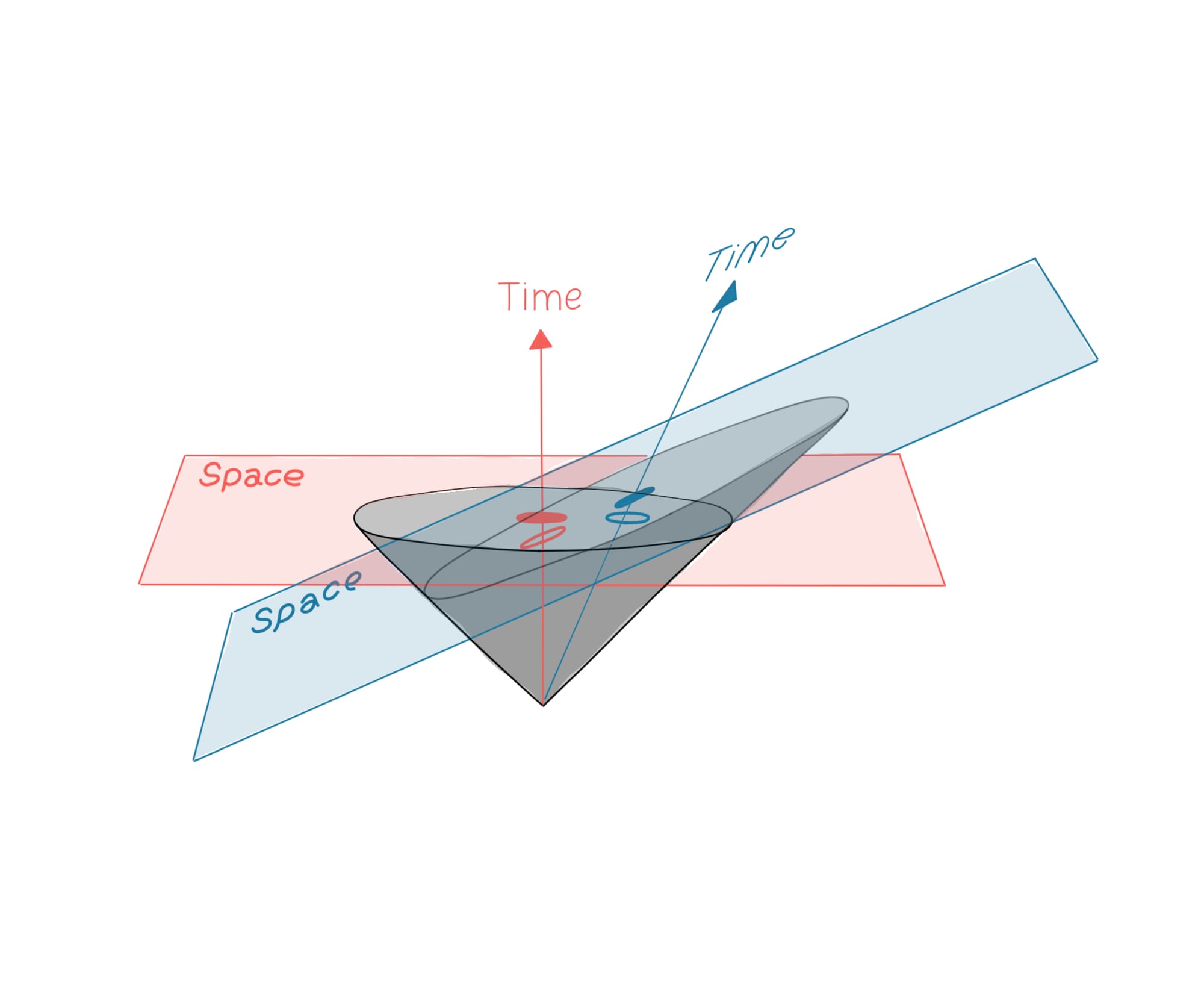
Here is an edited version of Minkowski space so that it shows the paradox at hand. The red and the blue axis represent what each of the two clocks A and B represent respectively. Movement is represented by a change in the horizontal coordinates over the vertical time. The two cones represent the distance light has travelled and therefore the maximum displacement possible at a given time (similar to the classical representation). Clock A experiences time on the horizontal plane whilst clock B experiences it on the slanted plane. Think about the different distances that light has to travel in each of the clocks. When one oscillation completes on the red time axis (coloured red circle), it sees the unfinished oscillation in clock B (uncoloured blue circle) the clock on the blue time axis still has not completed its oscillation as the light must travel a longer distance. Clock B actually ticks later at (coloured blue circle), As a result, clock B ticks slow from clock A's perspective. The opposite is true for clock A from clock B's perspective.
Time dilation due to a non-inertial frame of reference
The equivalence principle states that:
The gravitational "force" as experienced locally while standing on a massive body (such as the Earth) is the same as the pseudo-force experienced by an observer in a non-inertial (accelerated) frame of reference.
Therefore, the force experienced due to gravity is indistinguishable from the force experienced due to acceleration. Acceleration can be described as the rate of change of velocity (which we already know dilates time to a stationary observer). The special thing about acceleration is that it is a continuous and instantaneous refinement to velocity. Objects cannot distinguish between inertial time frames but can feel when they are altered. An accelerating clock will be at motion relative to itself and therefore time dilation due to a non-inertial frame is consistent to all observers. This causes time to slow down near massive objects where the gravitational pull is stronger.


