Using Python to Model Rainbows

The rainbow is a natural optical scattering and dispersion phenomenon that reveals the visible spectral composition of sunlight in the shape of an arc.  For the rainbow phenomenon, when the sun shines on water in a mist, the incident angle is almost the same for all waterdrops. Due to the geometrical similarity and symmetry of the water droplets, the light is scattered and dispersed by refraction.  

The rainbow consists of the primary rainbow, the secondary rainbow, and Alexander's dark space between the primary and secondary rainbows. The nature of a rainbow can be essentially explained with basic wave phenomena, such as refraction and reflection (Snell's law), polarisation, and diffraction. 

The model used in this project is based upon the scattering of the light in a spherical water droplet. I also assumed that all the droplets are of equal radius and have a uniform refractive index. Refractive index between raindrops and the atmosphere is closely related to the rainbow, especially the viewing angle of it. 

The model can be adjusted to different droplet size and refractive index.  

Introduction 

To model a rainbow, it is essential to understand how the shape, size and constitution of the liquid droplets affect them and how they form the primary and secondary rainbows. 

A collection of suspended water droplets in the atmosphere serves as a refractor of light. The water represents a medium with a different optical density than the surrounding air. Light waves refract when they cross over the boundary from one medium to another. The decrease in speed upon entry of light into a water droplet causes a bending of the path of light towards the normal. And upon exiting the droplet, light speeds up and bends away from the normal. The droplet causes a deviation in the path of light as it enters and exits the drop. 

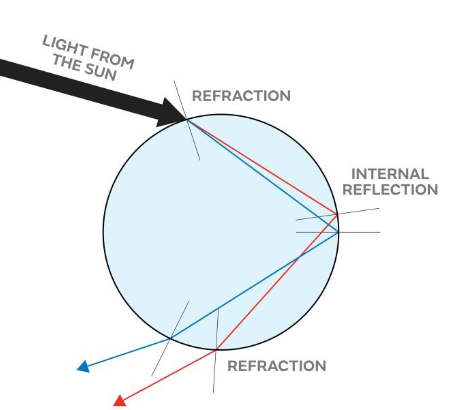
There are countless paths by which light rays from the sun can pass through a drop. Each path is characterized by this bending towards and away from the normal. One path of great significance in the discussion of rainbows is the path in which light refracts into the droplet, internally reflects, and then refracts out of the droplet.  

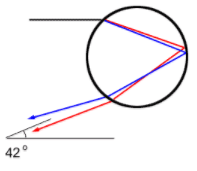
A light ray from the sun enters the droplet with a slight downward trajectory. Upon refracting twice and reflecting once, the light ray is dispersed and bent downward towards an observer on earth's surface. As in the case of the refraction of light through prisms with nonparallel sides, the refraction of light at two boundaries of the droplet results in the dispersion of light into a spectrum of colours. The shorter wavelength blue and violet light refract a slightly greater amount than the longer wavelength red light. Since the boundaries are not parallel to each other, the double refraction results in a distinct separation of the sunlight into its component colours. 

Both the primary and secondary rainbows are formed by the reflection and refraction of sunlight in tiny water droplets. When a sunbeam is being refracted twice and reflected once by the droplet, a primary rainbow will form. If the beam is being refracted twice and reflected twice, a secondary rainbow will form. As the secondary rainbow is formed by one more reflection than the primary rainbow, it is much fainter and rare to see. On the other hand, since the paths of sunbeams in a primary rainbow and a secondary rainbow are different, the colours of the secondary rainbow are arranged in just the reverse order of the primary one.

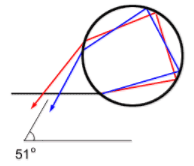
Overview & Specifications

The basic concept of the model adopted in this article is a simple calculation of the variables involved and fundamental equations based upon the refractive properties.  

As a result , the project will display a simple model of comparing the formation of  primary (Blue) rainbow and the secondary (Purple) rainbow.  

Snell’s law 

Snell’s law of refraction of light between two mediums of two materials  

\[ n_2 sin θ_i = n_1 sin θ_r \]

\[ θ_r = \frac{sin θ_i}{n} \]

Where \( n = \frac{n_2}{n_1} \) i.e. refractive index of water w.r.t air. 

Critical Angle  

\[c = sin^{-1} (\frac{1}{θ_r})\]

Obviously, if the angle of incidence > critical angle, there is no rainbow.

Deviation angle for primary rainbow 

Deviation angle for the primary rainbow can be calculated as a difference between the incident and refracted angle. 

\[\frac{D_p}{2} = (θ_i - θ_r)\]

\[D_p = 2sin^{-1}(\frac{1- {sin θ_i}}{n})\]

Deviation angle of secondary rainbow 

 Due to reflection law, deviation angle of secondary rainbow  

\[D_p = 180 - D_s\]

The rainbow angle is the minimum value of the scattering angle. 

Airy Theory 

Using Airy theory, the intensities (amplitude) of the primary and secondary rainbows are: 

\[I = (1 + cos(s-D))^2\]

Where I is the intensity, s is the scattering angle and D is the angle of deviation for the individual rainbow.

Building a Complete ‘Simple’ Model: 

Using the functions and equations above, a simple model and data set was created and the primary and secondary rainbows for different incident angles were plotted.  

calculate_primary_rainbow: This function calculates the angular positions of colours in a primary rainbow for a given angle of incidence, refractive index of the medium (water), and droplet radius. It accounts for the deviation angle which the light rays undergo after refraction and reflection inside the droplet. The function returns a set of angles corresponding to different colours based on dispersion. 

calculate_secondary_rainbow: Similar to the primary rainbow, this function computes the angular positions for a secondary rainbow. The secondary rainbow is formed due to two internal reflections within the droplet, and it appears at different angles compared to the primary. 

calculate_intensity_vs_angle: This function calculates the light intensity distribution as a function of scattering angles for both primary and secondary rainbows using an approximate model (Airy's theory). It provides insights into how bright each part of the rainbow is likely to appear. 

Model execution & Results: 

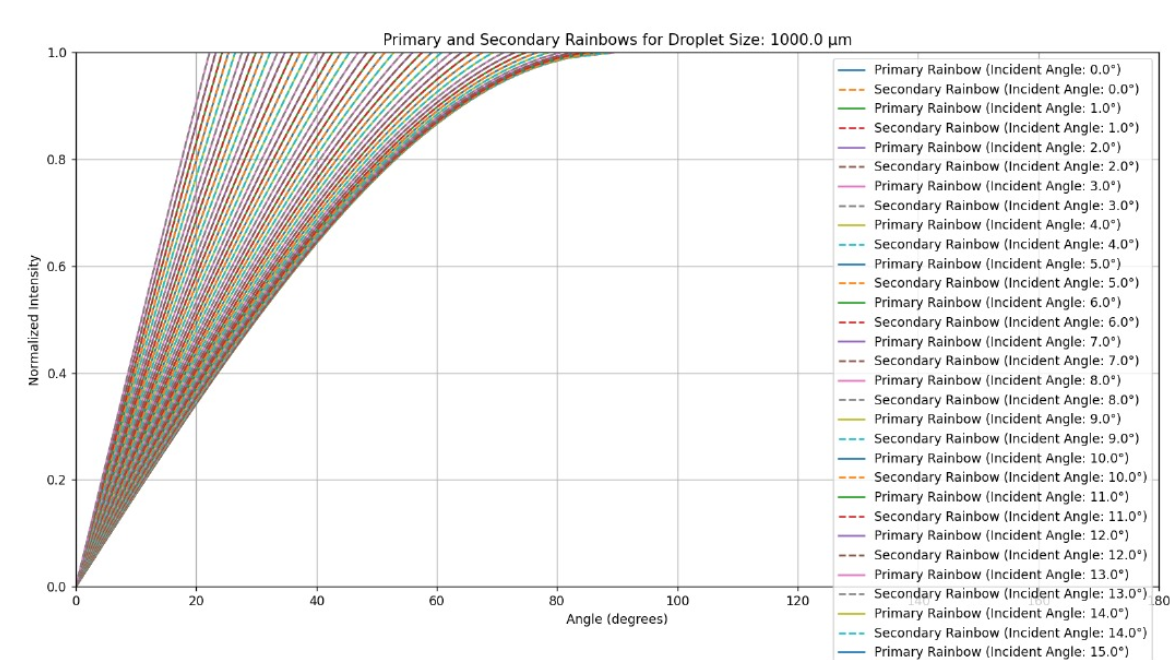
The script plots the angular positions of colours for primary and secondary rainbows as a function of the angle of incidence. It uses a loop to calculate and plot rainbows for different incident angles. Each type of rainbow is represented by a different line style in the plot.  

The model iterates through a range of angles of incidence from 0 to 90 degrees and computes the positions of primary and secondary rainbows for each angle. 

The plots are labelled and displayed with proper axes and titles to provide clarity on what is being visualized. 

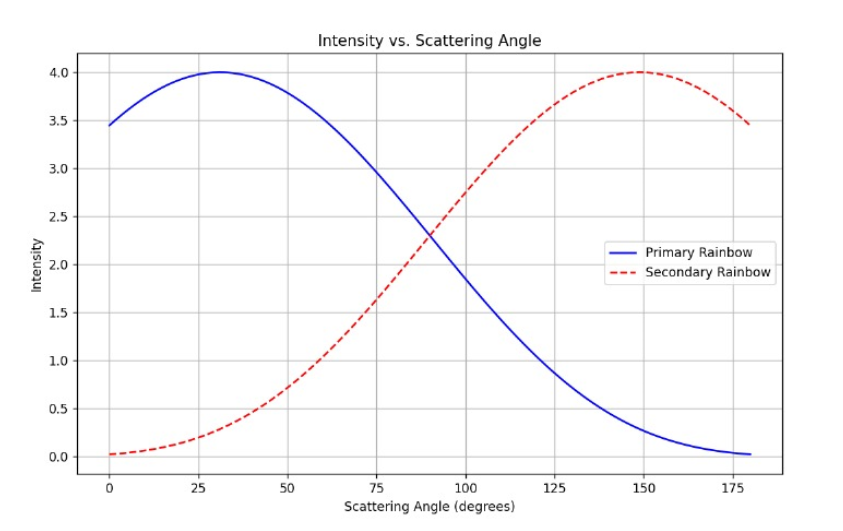
After examining the angular positions, the script calculates and plots the intensity distributions for a specific incident angle using the calculate_intensity_vs_angle function. This provides a visual representation of how the light intensity varies across different scattering angles for primary and secondary rainbows. 

This plot displays the intensity patterns for a specific angle of incidence (40 degrees in this example) for both the primary and secondary rainbows. 

The Rainbow Model (the Code) 

import numpy as np
import matplotlib.pyplot as plt

def calculate_primary_rainbow(angle_of_incidence, refractive_index, droplet_radius):
    # Convert angle to radians
    angle_of_incidence_rad = np.radians(angle_of_incidence)
    
    # Calculate critical angle
    critical_angle = np.arcsin(1 / refractive_index)
    
    # Check if critical angle is exceeded
    if angle_of_incidence_rad > critical_angle:
        return None  # Total internal reflection occurs, no rainbow
    
    # Calculate deviation angle for primary rainbow
    deviation_angle = 2 * np.arcsin((1 - np.sin(angle_of_incidence_rad)) / refractive_index)
    
    # Calculate angular positions of rainbow colors
    rainbow_angles = np.degrees(np.arcsin(np.linspace(0, 1, 100) * np.sin(deviation_angle)))
    
    return rainbow_angles

def calculate_secondary_rainbow(angle_of_incidence, refractive_index, droplet_radius):
    # Convert angle to radians
    angle_of_incidence_rad = np.radians(angle_of_incidence)
    
    # Calculate critical angle
    critical_angle = np.arcsin(1 / refractive_index)
    
    # Check if critical angle is exceeded
    if angle_of_incidence_rad > critical_angle:
        return None  # Total internal reflection occurs, no rainbow
    
    # Calculate deviation angle for primary rainbow
    deviation_angle_primary = 2 * np.arcsin((1 - np.sin(angle_of_incidence_rad)) / refractive_index)
    
    # Calculate deviation angle for secondary rainbow
    deviation_angle_secondary = np.pi - deviation_angle_primary
    
    # Calculate angular positions of rainbow colors for secondary rainbow
    rainbow_angles_secondary = np.degrees(np.arcsin(np.linspace(0, 1, 100) * np.sin(deviation_angle_secondary)))
    
    return rainbow_angles_secondary

def calculate_intensity_vs_angle(angle_of_incidence, refractive_index, droplet_radius):
    # Convert angle to radians
    angle_of_incidence_rad = np.radians(angle_of_incidence)
    
    # Calculate critical angle
    critical_angle = np.arcsin(1 / refractive_index)
    
    # Check if critical angle is exceeded
    if angle_of_incidence_rad > critical_angle:
        return None, None, None  # Total internal reflection occurs, no rainbow
    
    # Calculate deviation angle for primary rainbow
    deviation_angle_primary = 2 * np.arcsin((1 - np.sin(angle_of_incidence_rad)) / refractive_index)
    
    # Calculate deviation angle for secondary rainbow
    deviation_angle_secondary = np.pi - deviation_angle_primary
    
    # Calculate scattering angles for intensity calculation
    scattering_angles = np.linspace(0, np.pi, 100)
    
    # Calculate intensity using Airy theory
    intensity_primary = (1 + np.cos(scattering_angles - deviation_angle_primary))**2
    intensity_secondary = (1 + np.cos(scattering_angles - deviation_angle_secondary))**2
    
    return np.degrees(scattering_angles), intensity_primary, intensity_secondary

# Parameters
refractive_index_water = 1.333  # Refractive index of water

# Incident angle range (in degrees)
incident_angles = np.linspace(0, 90, 91)

# Droplet size in micrometers
droplet_size = 1000.0  # Adjusted to test different droplet sizes

# Plotting primary and secondary rainbows for different incident angles
plt.figure(figsize=(10, 6))

for angle in incident_angles:
    rainbow_angles = calculate_primary_rainbow(angle, refractive_index_water, droplet_size)
    if rainbow_angles is not None:
        plt.plot(rainbow_angles, np.linspace(0, 1, len(rainbow_angles)), label=f'Primary Rainbow (Incident Angle: {angle}°)')
    
    rainbow_angles_secondary = calculate_secondary_rainbow(angle, refractive_index_water, droplet_size)
    if rainbow_angles_secondary is not None:
        plt.plot(rainbow_angles_secondary, np.linspace(0, 1, len(rainbow_angles_secondary)), linestyle='--', label=f'Secondary Rainbow (Incident Angle: {angle}°)')

plt.xlabel('Angle (degrees)')
plt.ylabel('Normalized Intensity')
plt.title(f'Primary and Secondary Rainbows for Droplet Size: {droplet_size} μm')
plt.xlim(0, 180)
plt.ylim(0, 1)
plt.legend()
plt.grid(True)
plt.show()

# Calculate intensity vs. scattering angle for a specific incident angle
angle_of_incidence_example = 40  # Example incident angle in degrees
scattering_angles, intensity_primary_example, intensity_secondary_example = calculate_intensity_vs_angle(angle_of_incidence_example, refractive_index_water, droplet_size)

# Plotting intensity vs. scattering angle
plt.figure(figsize=(10, 6))
plt.plot(scattering_angles, intensity_primary_example, color='blue', label='Primary Rainbow')
plt.plot(scattering_angles, intensity_secondary_example, color='red', linestyle='--', label='Secondary Rainbow')
plt.xlabel('Scattering Angle (degrees)')
plt.ylabel('Intensity')
plt.title("Intensity vs. Scattering Angle")
plt.legend()
plt.grid(True)
plt.show()

Conclusion 

In this model, I used spherical droplets of the same size and uniform optical properties such as refractive index. However, the model can be simulated for different sized droplets as well as droplets with differing refractive indexes. 

The program finally displays two plots: one showing how the angular positions of rainbows change with varying incident angles and illustrates how primary and secondary rainbows form as functions of the angle of incidence, and another showing the intensity distribution for a specific angle of incidence. 

This helps understand the optical phenomena involved in the formation of rainbows and the impact of different physical parameters like droplet size and refractive index. 

Limitations & Further development 

This model has number of limitations which can be improved in the future. One major limitation is the assumption of spherical droplets. In reality, bigger droplets are not completely spherical. Diffraction and polarisation are also not properly explored in this model.