Physics

Einstein's Field Equations

Einstein's Field Equations are among the most famous equations in all of physics, and yet what do they describe, and how do they work?

William Moore

25 Mar 2025 — 12 min read

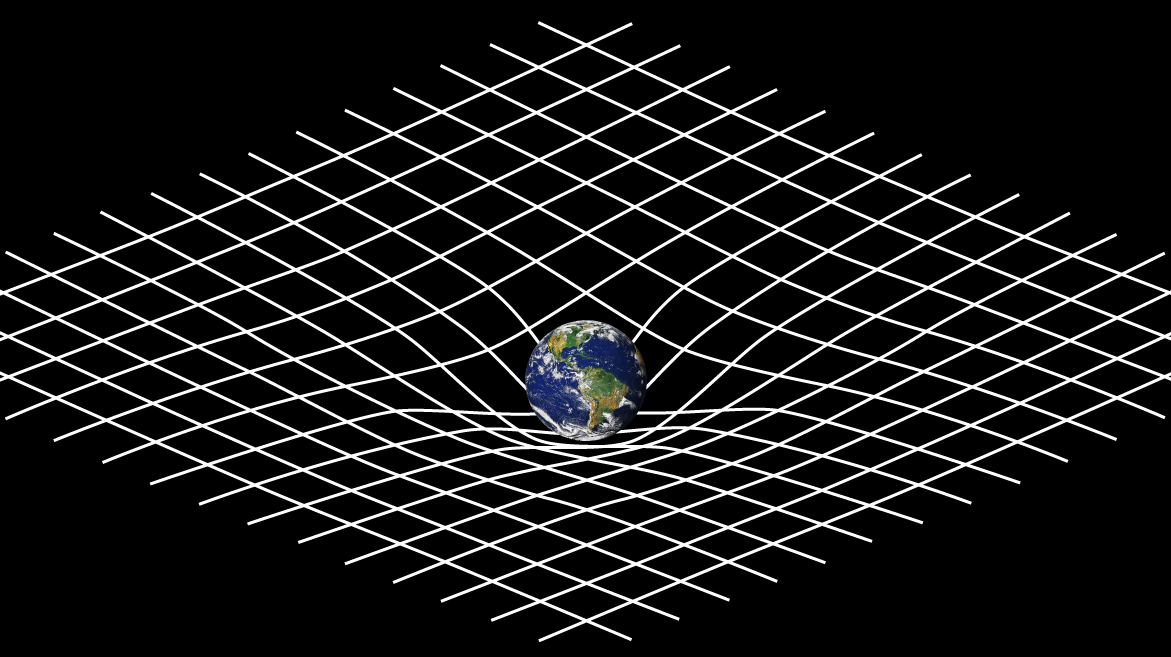
Introduction

Einstein's field equations describe how objects affect space time and in turn how space time affects objects. They explain the apparent forces of gravity, gravitational waves, black holes, and the accelerating expansion of the universe. In order to understand Einstein’s field equations, one must start from the beginning. At age 16, whilst studying in Aarau, he conducted a famous thought experiment where he imagined a spaceship with no windows accelerating at a constant 9.8m/s2 through space. To the person inside the spaceship, it would appear as if they were still on earth with gravity acting upon them. He figured that when he was accelerating upwards, everything around him would appear to accelerate downwards at 9.8m/s2, the same as on earth. To the inside observer, there would be no experiment that could discern the difference. Einstein used this thought experiment to propose a theory that acceleration has the exact same effect as gravity. This is called the principle of equivalence.

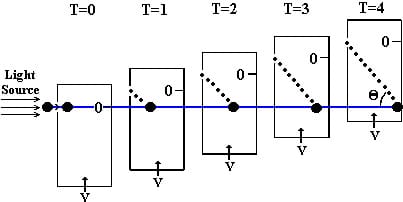
Picture this, the spaceship is at a standstill in space with a light bulb on the left side of it. As the light turns on, photons of light travel out and move to the right, and the spaceship starts to accelerate. To an outside observer, the photons of light travel sideways in a straight line while the spaceship is moving upward. To an observer inside the spaceship, both them and the spaceship are moving upward, so relative to them, the light appears to be traveling downward in a curve. Einstein used the principles we established in the first paragraph to state that since acceleration and gravity have the same effect, gravity would also appear to curve light.

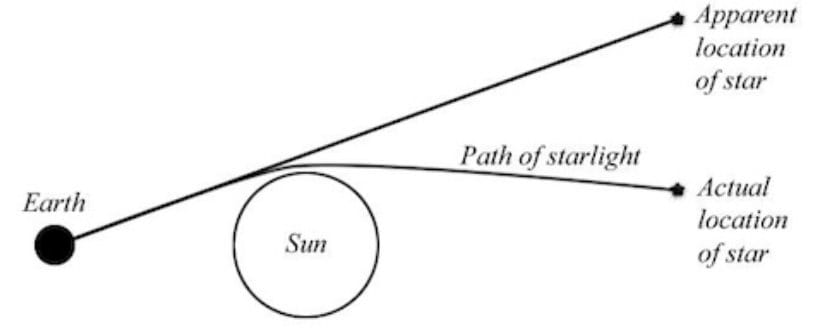
This was just a theory until the 29th of May 1919 when astronomers observed the bending of light during a solar eclipse. This was a huge shock to the scientific community as it not only proved Einstein right, but also proved that Newtons theories were incorrect. Newton's equation, $F=G\frac{m_1 m_2}{r^2}$ that the gravitational force of attraction between two objects was proportional to the mass of the mass of both objects. Einstein's recent discovery showed that photons could still be influenced by gravity even though they had no mass. This prompted Einstein to wonder how gravity really worked, which led to some of the most ground-breaking scientific discoveries in the last century.

What is space-time

Einstein's theory was that massive objects could bend and warp space-time and that particles were not necessarily being attracted by the objects, but simply were trying to take the shortest path.

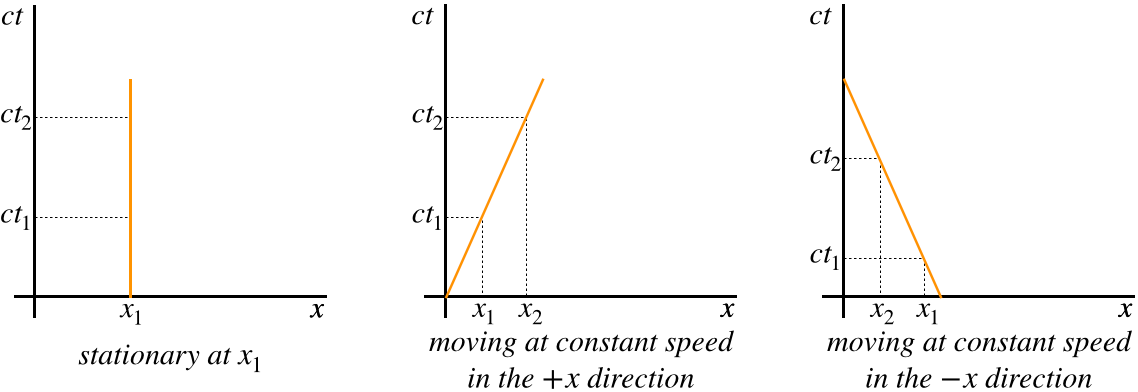
Whilst space-time might sound like fiction, Einstein believed that it is in fact very real. Einstein thought of space time as a way to represent the complex relationship between space and time using four dimensions. If you don't understand, consider the following: We can imagine space and time as two dimensions on a graph, the x and y axis. If an object is not in motion, it will not change on the y axis, it will however keep on moving up the x axis as it continues to travel through time. As an object moves through space at a constant speed, the distance it travels is proportional to the time taken to travel that distance and so it would appear as a vertical line on the graph. The faster the object is moving, the more the gradient decreases. If an object is accelerating, the line we would see on the graph is a curve. Going back to the introduction, we know that gravity has the same effect as acceleration, and therefore an object under the influence of gravity would also take a curved path through space time.

Einstein's Field Equation

Einstein's Field Equations look this:

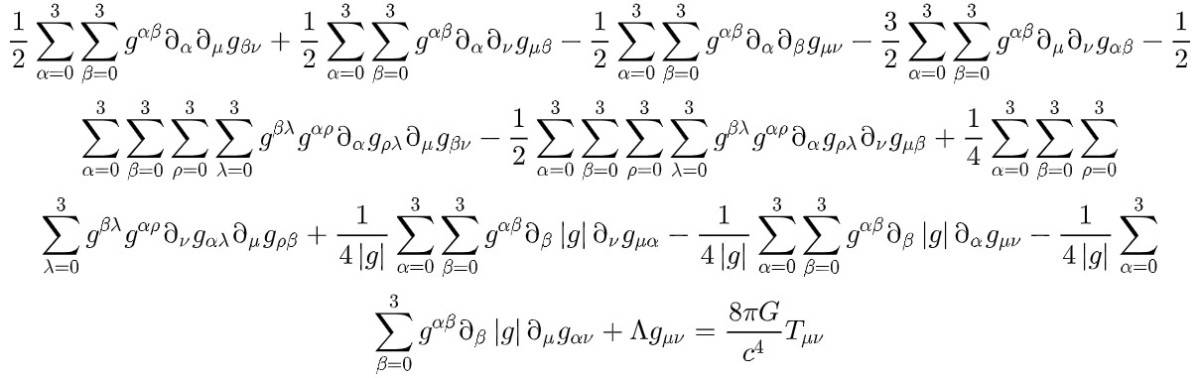
But can be condensed into one line using the Einstein summation convention:

\[R_{\mu\nu} - \frac{1}{2}g_{\mu\nu}R + g_{\mu\nu}\Lambda = \frac{8\pi G}{c^4} T_{\mu\nu}\]

So What does this actually mean?

$R$ is the Ricci scalar

$R_{\mu \nu}$ is the Ricci tensor

$g_{\mu \nu}$ is the metric tensor

$\Lambda$ is the cosmological constant

$T_{\mu\nu}$ is the Stress-Energy Tensor

Everything on the left of this equation refers to the curvature of space time, everything on the right of the equation refers to mass and energy. In short, Mass tells space-time how to curve and space-time tells mass how to move.

What is a Metric Tensor?

In general, A metric tensor can be used to describe the shape of a manifold. In the field equations, a metric tensor is used to describe the curved space-time.

Picture in your mind a mountain range and a person standing on top of one of the mountains. The person will have coordinates $x^0$ and $x^1$ referring to how far north and east they are and a coordinate $\theta$ to describe their height above sea level. If we want to calculate how the height of the person would change if they moved along the $x^0$ axis, we would multiply the gradient of the line $\frac{\delta\theta}{\delta x^0}$ with the distance moved $\delta x^0$ giving the equation:

\[\delta\theta_{x^0} = \frac{\delta\theta}{\delta x^0}\times\delta x^0\]

in order to work out the change in height if we travel diagonally (in both the $x^0$ and $x^1$ direction), we can treat these movements as vectors and simply add them.
where $s$ is the diagonal movement:

\[\delta\theta_s = \frac{\delta\theta}{\delta x^0}\delta x^0 + \frac{\delta\theta}{\delta x^1}\delta x^1\]

In planes with higher dimensions:

\[\delta\theta = \sum_n\frac{\delta\theta}{\delta x^n}\delta x^n\]

The problem with relativity is that time and distances can change depending on the frame of reference. In order for an equation to be universally true, it must be true in all reference frames. Going back to the mountain range, the person could be standing at one coordinate on the $(x^0,x^1)$ frame of reference, but in the $(y^0,y^1)$ frame of reference they could be at a different coordinate. Whilst the position hasn't changed, the coordinates would differ because they are in different frames of reference.

However, not all hope is lost. If we plot a point using $(y^0,y^1)$, we can still express the value of $y^0$ or $y^1$ as a coordinate on the $(x^0,x^1)$ frame of reference. If we know all of the gradients of the $x$ frame of reference, we can figure out the gradients in the $y$ frame by using the chain rule. We can choose any value of $y^n$ to use for this equation:

\[\frac{\delta\theta}{\delta y^0} = \frac{\delta\theta}{\delta x^0}\frac{\delta x^0}{\delta y^0} + \frac{\delta\theta}{\delta x^1}\frac{\delta x^1}{\delta y^0}\]

In higher dimensions:

\[\frac{\delta\theta}{\delta y^n} = \sum_m\frac{\delta\theta}{\delta x^m}\frac{\delta x^m}{\delta y^n}\]

There are many different forms of tensors in mathematics. Scalars are rank 0 tensors because they just consist of magnitude. Vectors are rank 1 tensors because they have magnitude and direction. In order to transfer a vector from the $x$ to $y$ frames of reference, we can alter equation 4 which we used to work out the change in height when moving diagonally.

\[V_y^n = \sum_m\frac{\delta y^n}{\delta x^m}V_x^m\]

Unfortunately, the metric tensor which Einstein uses in this equation is a rank 2 tensor this means that it describes the fixed relationship between two vectors. For example, if we put a block against a wall and force is applied parallel to the wall, it moves a certain distance in the $x^0$ direction, the work done is equal to the force applied times the distance travelled

\[W = F \times \delta x^0\]

However, if the force is applied at an angle, the equation is

\[W = F \cos{\alpha} \times \delta x^0\]

You will notice that if the force is applied perpendicular to the wall, at a 90 degree angle, $\cos{90}=0$ and there is no work done. This is the same no matter which frame of reference you look at it from. The force and distance can be considered as vectors, having both magnitude and direction. The work done can be considered a tensor, describing the relationship between the force and the distance moved.

If we take the $m$th coordinate of vector $A$, and combine it with the $n$th coordinate of vector $B$, we get the tensor $T^{nm}$. In two dimensional space, the values of $m$ and $n$ can be either one or two, so there are 4 possible values for $T^{nm}$. Einstein's Field Equation describes four dimensional space and so there are 16 values for the metric tensor. If we want to find out what the vectors $A_y^m$ and $B_y^n$ are in the x frame of reference, we can use equation 7 but replace $V$ with our vectors $A$ and $B$:

\[A_y^mB_y^n = \sum_r\frac{\delta y^m}{\delta x^r}A_x^r \sum_s\frac{\delta y^n}{\delta x^s}B_x^s\]

If we rearrange and use our tensor, we get:

\[T_y^{mn} = \sum_{rs}\frac{\delta y^m}{\delta x^r}\frac{\delta y^n}{\delta x^s}T_x^{rs}\]

This is called the contra-variant transformation. Einstein's Equations use the covariant transformation which changes the notation and flips the $\frac{dy}{dx}$ terms and changes the position of the indices on the tensor. It looks like this:

\[T_{mn}(y) = \sum_{rs}\frac{\delta x^r}{\delta y^m}\frac{\delta x^s}{\delta y^n}T_{rs}(x)\]

In 2 dimensional euclidean geometry, Pythagoras theorem states that for a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. We can use this to find out the length of a vector using the change of $x^0$ and $x^1$ coordinates

\[\delta {x^0}^2+\delta {x^1}^2=\delta s^2\]

For higher dimensions:

\[\sum_m\delta x^m\delta x^m=\delta s^2\]

If we complicate this further, we can get:

\[\delta s^2 = \delta_{mn}\sum_{mn}\delta x^m\delta x^n\]

The $d_{mn}$ in this equation refers to the Kronecker Delta. The Kronecker Delta has a value of zero if $m$ does not equal $n$, allowing us to exclude values which are not in the original Pythagorean theorem.

If we use equation 4 to find what $\delta x^m$ and $\delta x^n$ are equal to we get:

\[\delta x^m = \sum_r\frac{\delta x^m}{\delta y^r}\delta y^r\]

And:

\[\delta x^n = \sum_s\frac{\delta x^n}{\delta y^s}\delta y^s\]

If we substitute these into equation 15 we get:

\[\delta s^2 = \delta_{mn}\sum_{rs}\frac{\delta x^m}{\delta y^r}\delta y^r\frac{\delta x^n}{\delta y^s}\delta y^s\]

Rearranging we get:

\[\delta s^2 = \delta_{mn}\sum_{rs}\frac{\delta x^m}{\delta y^r}\frac{\delta x^n}{\delta y^s}\delta y^r\delta y^s\]

$\delta_{mn}\sum_{rs}\frac{\delta x^m}{\delta y^r}\frac{\delta x^n}{\delta y^s}$ is what we call the metric tensor, Einstein refers to this in his equation as $g_{\mu\nu}$. rewriting Pythagoras theorem with the metric tensor it would look like this:

\[\delta s^2 = g_{mn}\delta y^r\delta y^s\]

Looking back to equation 15, we can see that the metric tensor and the Kronecker delta have the same value. and this is true as long as we are talking about Euclidean geometry. In non Euclidean geometry, Pythagoras theorem does not stand true and so the metric tensor is used to correct Pythagoras theorem to account for non Euclidean geometry. In Einstein's equation, the metric tensor appears with the cosmological constant which allows space-time to curve, even when in an absence of matter.

Cristoffel symbol and the Ricci Tensor

The Cristoffel symbol $\Gamma^{\mu}_{\beta\alpha}$ is a mathematical symbol used to describe how basis vectors of a coordinate system change from point to point in curved space. Whilst the Cristoffel symbol does not explicitly appear in the field equations, it is heavily featured in the definition of the Ricci Tensor. The Cristoffel symbol can be defined in terms of the metric tensor and its derivatives:

\[\Gamma^\mu_{\nu\lambda}=\frac{1}{2}g^{\mu\sigma}(\partial\nu g_{\sigma\lambda}+\partial_\lambda g_{\sigma\nu}-\partial_\sigma g_{\nu\lambda})\]

The Cristoffel symbol is used in the covariant derivatives that were shown in the last section. In a Cartesian coordinate system the ordinary derivative $\partial_\nu V^\mu$ does not produce a tensor because the basis vectors change as you move across space. The Cristoffel symbols capture this variation and correct the ordinary derivative in order for it to produce a tensor in a curved space. In flat space, the metric tensor can be substituted for the Kronecker delta which holds a value of either one or zero. The derivative of the Kronecker is zero and thus the Cristoffel symbols vanish. The Cristoffel symbols are not tensors themselves as they depend on the choice of coordinates, they do however appear in the definition of the Riemann tensor.

\[R^m_{ikp}=\frac{\partial\Gamma^m_{ik}}{\partial xp}-\frac{\partial\Gamma^m_{ip}}{\partial x^k}+\Gamma^r_{ik}\Gamma^m_{rp}-\Gamma^r_{ip}\Gamma^m_{rk}\]

The Riemann tensor is a rank 4 tensor Measures intrinsic curvature, tracks how vectors change under parallel transport, distinguishes flat spaces from curved spaces and serves as the foundation of spacetime geometry in general relativity. In essence, the Riemann tensor encodes the geometry of a space and reveals how that geometry interacts with the objects within it. The Ricci tensor is a contraction of the Riemann tensor on its first and third indices. The Ricci tensor can be obtained by summing over the repeated indices.

\[R_{\mu\nu}=R^\rho_{\mu\rho\nu}\]

substituting the definition of the Riemann tensor into the contraction, we can produce the Ricci tensor in terms of the Cristoffel symbols:

\[R_{\mu\nu} = \partial_\rho \Gamma^\rho_{\mu\nu} - \partial_\nu \Gamma^\rho_{\mu\rho} + \Gamma^\rho_{\rho\lambda} \Gamma^\lambda_{\mu\nu} - \Gamma^\rho_{\nu\lambda} \Gamma^\lambda_{\mu\rho}\]

The Ricci tensor describes the change in volume of a space-time object using geodesics. A geodesic is essentially the shortest path an object can take through a curved space time and the Ricci tensor describes how geodesics converge or diverge. In other words, if you were to run two parallel geodesics close to each other, the lines would eventually get further or closer together because of the curvature of space-time. The Ricci tensor would measure the distance between these lines, and use that to work out the change in volume. All objects move through space time in geodesics therefore the Ricci tensor is essential for the Field equations. Contracting the Riemann tensor further produces the Ricci scalar $R$ which is a single number that measures the curvature at a point. the Ricci scalar ensures that energy conservation is properly included in the equations.

Stress-Energy Tensor and the Einstein gravitational constant

The stress energy tensor $T^{\mu\nu}$ is a rank 2 tensor which describes the density and flux of energy and momentum in spacetime as well as sheer stress and pressure. In 4 dimensional space, the symbols $\mu$ and $\nu$ take on the values 0, 1, 2 and 3 and since the tensor is rank 2, they can displayed neatly in a 4x4 grid:

In this format,
$T^{01}$,$T^{02}$,$T^{03}$ describe momentum density
$T^{21}$,$T^{31}$,$T^{32}$ describe momentum flux
$T^{10}$,$T^{20}$,$T^{30}$ describe energy flux
$T^{00}$ describes energy density
$T^{12}$,$T^{13}$,$T^{23}$ describe shear stress
$T^{11}$,$T^{22}$,$T^{33}$ describe pressure

The Tensor shown here is in contravariant form. Einstein uses the covariant form which can be related using the metric tensor which allows for indices to be raised and lowered.

\[T_{\mu\nu}=g_{\mu\alpha}g_{\nu\beta}T^{\alpha\beta}\]

The Einstein gravitational constant ($\frac{8\pi G}{c^4}$) converts the units of the stress-energy tensor so that both sides of the equation match. The G represents Newtons gravitational constant and the $8\pi$ comes from the result of integrating over a spherically symmetric gravitational field. The Einstein gravitational constant is such a small number because the $8\pi G$ is put over the speed of light to the power of four. this is the reason why gravity is by far the weakest of all the fundamental forces. The stress energy tensor, in combination with the Einstein gravitational constant, describes how energy and momentum act as a source of curvature in spacetime.

Conclusion

Combining all that we have learnt, we now know what the Einstein field equations are and hopefully describe what it all means Einstein's equations have had a massive impact of the scientific world. It replaced newtons ideas of gravity, predicted black holes and gravitational waves, explained mercury’s puzzling orbit, and led to the big bang theory. Don’t be afraid if you don’t understand yet, it took the smartest man in the world many years to come up with his equations.