Chaos Theory

Introduction

The natural world is filled with complex and unpredictable phenomena, from weather patterns to the dynamics of ecosystems and the stock market. At first glance, these systems may seem entirely random, yet there are often underlying deterministic laws governed by mathematics. Chaos Theory, a branch of mathematics, provides a framework for understanding these seemingly erratic behaviour’s by revealing the sensitive dependence on initial conditions that governs many nonlinear systems.

First formalised in the mid-20th century, Chaos Theory challenges traditional ideas of predictability, demonstrating how small, seemingly insignificant differences in initial conditions can lead to drastically different outcomes—a concept popularly known as the “butterfly effect.” Initially regarded as a curiosity, Chaos Theory has grown to become a cornerstone of modern science and engineering, finding applications in physics, biology, meteorology, economics, and beyond.

First, we will into the foundations of Chaos Theory, beginning with the mathematical principles that define it, such as deterministic chaos and nonlinear dynamics. Then, we'll explores key models like the Lorenz system, logistic maps, and fractals, which showcase chaos in action. Finally, the paper examines real-world applications of Chaos Theory, from weather forecasting to quantum mechanics, to economical application, highlighting its profound impact on how we understand and navigate complex systems.

The Mathematical principles of Chaos Theory and Edward Lorenz

At the heart of chaos theory lies the idea that deterministic systems, governed by mathematical equations, can exhibit behaviour so complex that it appears random. Chaos emerges from simple rules, making it a cornerstone of nonlinear dynamics. One of the most significant breakthroughs in this field was made by Edward Lorenz, a meteorologist and mathematician whose work illuminated the underlying principles of chaos theory. 

Edward Lorenz’s groundbreaking work on chaos theory began unexpectedly in 1961 while he was running weather simulations on a primitive computer at the Massachusetts Institute of Technology (MIT). Lorenz was using a basic weather model to predict atmospheric conditions, a system defined by a set of twelve nonlinear differential equations. One day, Lorenz decided that he wanted to rerun a simulation by manually inputting data from a previous run. However, instead of inputting the full six-decimal precision of the data, he rounded the numbers to three decimal places, assuming the difference was insignificant as the difference was less than a thousandth. To his surprise, the new simulation diverged dramatically from the original, even though the initial conditions were almost identical. They behaved similarly in the beginning but before long resulted in dramatically different outcomes.

This anomaly piqued Lorenz’s curiosity and led him to explore the sensitivity of systems to initial conditions—a property that would later become a cornerstone of chaos theory. His discovery demonstrated that small, seemingly negligible differences in starting points could lead to vastly different outcomes over time. Lorenz famously likened this phenomenon to a butterfly flapping its wings in Brazil, potentially causing a tornado in Texas, a metaphor that captured the public imagination and underscored the profound unpredictability inherent in chaotic systems.

To study this phenomenon further, Lorenz developed a simplified model consisting of three nonlinear differential equations. These equations describe the movement of fluid layers under convection, a process relevant to atmospheric dynamics. The system is given by:

\( \frac{dx}{dt} = \sigma(y - x) \),

\( \frac{dy}{dt} = x(\rho - z) - y \),

 \( \frac{dz}{dt} = xy - \beta z \).

Here:

​• x,y and z and are variables representing the state of the system such as temperature or pressure.

​• \( \sigma, \rho, \beta \) are parameters describing the system’s behaviour.

Through these equations, Lorenz uncovered a striking feature: a set of solutions that never repeat but remain confined within a bounded region of phase space. This structure, known as the Lorenz attractor, represents the system’s chaotic yet deterministic nature. Its iconic butterfly shape has become synonymous with chaos theory.

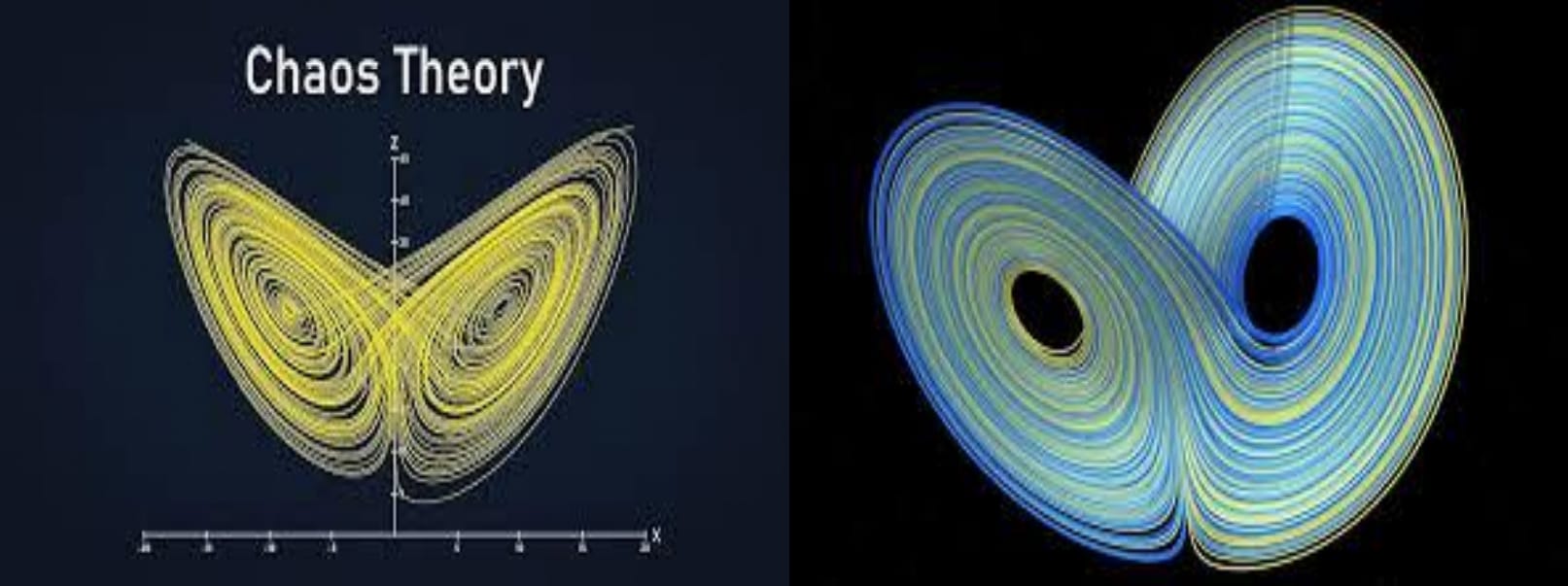
Lorenz’s discovery fundamentally challenged the prevailing deterministic view of the universe, which was that knowing the initial conditions of a system with infinite precision would allow one to predict its future indefinitely. Instead, his work revealed that in certain systems, small uncertainties grow exponentially, rendering long-term predictions impossible.

This principle, famously encapsulated by the metaphor of such a small, seemingly meaningless event such as butterfly flapping its wings and could result in an exponentially larger result, such as causing a hurricane weeks later, underscoring the profound implications of chaos theory not only in meteorology but across fields as diverse as biology, economics, and engineering.

Real world applications of chaos theory 

Chaos theory has transformed our understanding of complex, non-linear systems, offering valuable insights into areas where small changes lead to significant unexpected outcomes. From predicting the weather to understanding biological processes, chaos theory has been found useful in a variety of disciplines shaping the way we approach uncertainty and complex systems.

Weather forecasting

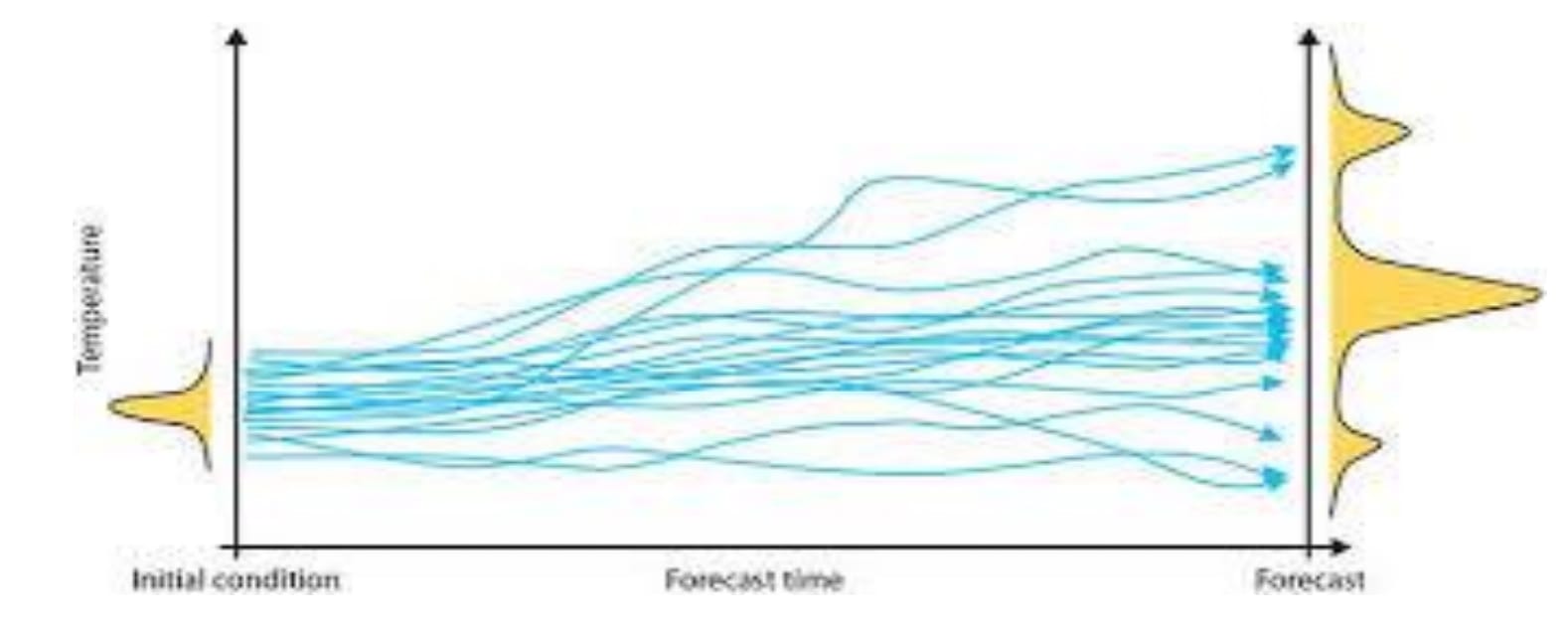
One of the most noticeable applications of chaos theory is predicting weather patterns, stemming from Edward Lorenz. His work demonstrated the inherent limitations in predicting the weather due to the extreme sensitivity of atmospheric systems to initialconditions and our lack of knowledge regarding these conditions. Tiny, immeasurableinputs of data such as a slight fluctuation in temperature of pressure can result in vastly different weather patterns over time. This sensitivity, encapsulated as the butterfly effect explains why predictions beyond a week often lose accuracy and despite the immense power of today's computers become nothing more than a guess. No matter how sophisticated our models or computers become chaos imposes an upper limit on how far into the future reliable predictions can be made. This is why we have a probabilistic approach to our forecasting rather than a deterministic one.

Financial markets

In financial markets, chaos theory offers a framework for understanding the apparent randomness of price movements. While traditional models often assume markets are efficient and follow a normal distribution, real-world data frequently exhibit irregularities, such as sudden spikes or crashes, that these models cannot adequately explain suggesting that while short term patterns may appear, the overall system is chaotic, making long term predictions incredibly unreliable. Chaos theory suggests that these anomalies arise from the complex, nonlinear interactions of numerous factors, including economic indicators, individual investor behaviours, and geopolitical events (to name a few). By recognising the market as a chaotic system, analysts can better appreciate its inherent unpredictability. Tools derived from chaos theory, such as strange attractors and fractal dimensions, have been employed to identify underlying patterns within seemingly erratic market data. For instance, the Fractal Market Hypothesis, introduced by Edgar E. Peters, suggests that financial markets are stable when participants have diverse investment horizons, and instability occurs when this diversity diminishes. This perspective challenges traditional financial theories and provides a nuanced understanding of market dynamics, emphasising the importance of diversity among investors to maintain market stability.   

Ecology

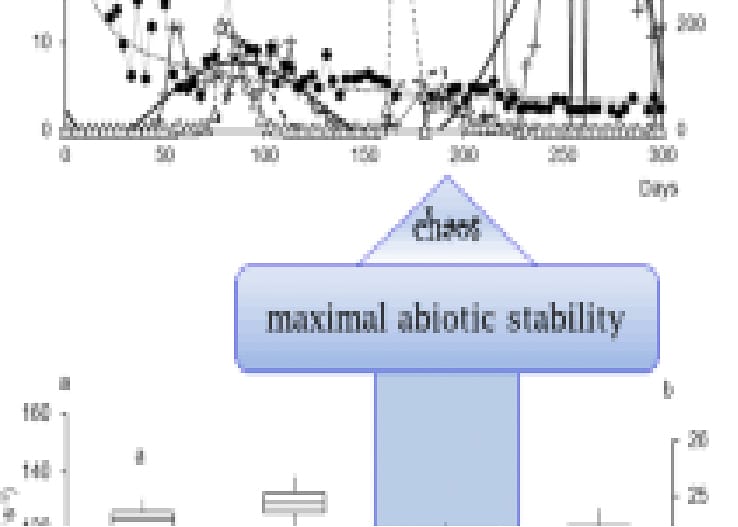
Ecology is another field where chaos theory has proven invaluable. Population dynamics, such as predator-prey relationships, often exhibit chaotic behaviour, with small changes in factors like birth rates, death rates or resource availability leading to dramatic shifts in population sizes. By applying chaos theory, ecologists can better understand and model these fluctuations, aiding in the conservation of ecosystems and species.

Medicine and biology

In medicine and biology, chaos theory plays a crucial role in understanding irregularities in biological rhythms, such as heartbeats and brain waves. Traditional linear models often fall short in capturing the unpredictable behaviours observed in biological systems whereas chaos theory offers a framework to understand and analyse these complexities. For example, arrhythmias or seizures often arise from complex interactions within chaotic systems. By modelling these processes through chaos theory, researchers have developed better diagnostic tools and treatments, improving patient outcomes. 

Engineering and technology

Finally, chaos theory plays a crucial role in engineering and technology by providing insights into complex, nonlinear systems. In control systems, it helps predict and mitigate erratic behaviours, enabling engineers to design stabilising controllers. In signal processing, chaos theory aids in filtering noise and improving signal clarity. Optimisation problems benefit from chaos-based methods to find efficient solutions in complex scenarios. Additionally, chaos engineering involves intentionally introducing failures into systems to identify vulnerabilities and enhance resilience, as exemplified by tools like Netflix’s “Chaos Monkey.”