Adaptations of GNSS

Of the 300+[^ https://www.newscientist.com/article/2290456-uk-night-skies-will-be-among-worst-hit-by-satellite-megaconstellations/] satellites observable at any time from the UK night sky, at least 12 of which can be tracked as part of the 31-strong, ~22,000km high American Global Positioning System[^https://www.garmin.com/en-GB/aboutgps/] This essay will explore various adaptations made for Global Navigation Satellite Systems (GNSS).

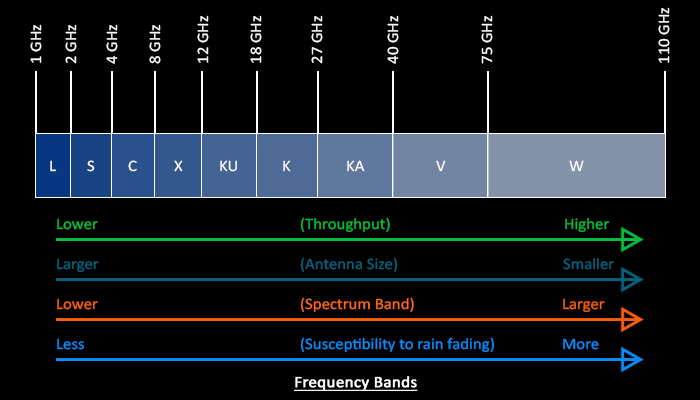
Satellite communications rely on the transmission of electromagnetic signals across vast distances from orbiting satellites to ground stations, of which the chosen frequency results from a compromise between bandwidth capacity against atmospheric attenuation, as a lower frequency is less susceptible to absorption by atmospheric factors such as water vapour, oxygen, and rain (rain fade).

The Free Space Path Loss equation is representative of this phenomenon, where signal strength diminishes with distance:

\[ \text{FSPL (dB)} = 20\log_{10}(d) + 20\log_{10}(f) + 32.45 \\~\\ d: \text{ distance between the transmitter and receiver (km)}  \\ f: \text{ frequency of the signal (MHz)} \]

This is why GPS uses the L1 and L5 band, which are more reliable. The recent addition of the L5 band allows for higher power transmissions, and lessened doppler shift*), while requiring more computational processing, provide superior robustness[^ https://pmc.ncbi.nlm.nih.gov/articles/PMC6165328/#sec2-sensors-18-02779].

BPSK

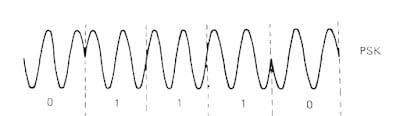
Once a signal is received, it is necessary to demodulate it. You may have heard of common modulation methods such as AM or FM (this being written at a time where the radio is still in use). Neither of these, however are used within GPS, which instead uses Binary Phase-Shift Keying (BPSK). This method shifts the carrier signal between two sates (0 and 180 degrees) to represent binary values, and allows for a higher noise resistance compared to other methods such as PSK, FSK and QAM (digital adaptations and a combination of AM and FM, respectively).[^ https://www.myadventuresinengineering.com/2019/05/understanding-bpsk-modulation.html] [^ https://www.geeksforgeeks.org/bpsk-binary-phase-shift-keying/]

\[ s(t) = A_c \cos(2\pi f_c t + \phi(t)) \\~\\ \phi(t) = 0 \text{ for binary "0"} \\ \phi(t) = \pi \text{ for binary "1"} \]

CDMA

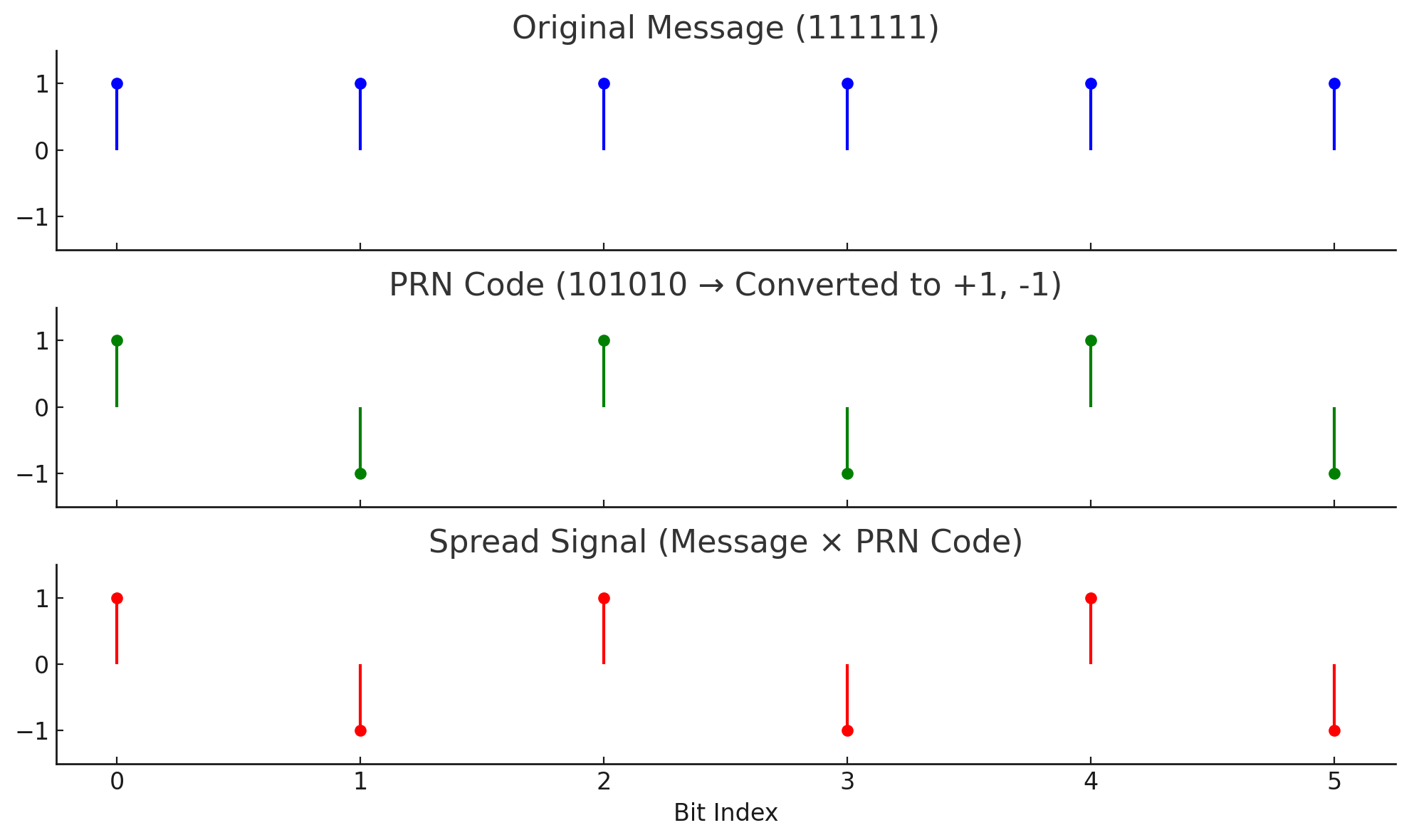
Given that at any time a GNSS receiver will be susceptible to signals from approximately 12 satellites, all at a similar band, there is a necessity to avoid wave interference. GPS employs Code Division Multiple Access (CDMA) to allow multiple satellites to transmit on the same frequency bands without interference. Each satellite is assigned a unique pseudo-random noise (PRN) code[^ https://skynet.ee.ic.ac.uk/notes/CS_2016_7A_PN_codes_PN_signals_and_SSComms.pdf with help from AI to explain it to the author], spreading the signal across a wide bandwidth. The receiver uses the PRN code to correlate and extract the intended satellite’s signal, effectively separating it from others.

In every GPS signal lies:

• Ephemeris Data: the precise orbital path of the satellite, allowing GNSS receivers to determine the satellite's position at any given time.
• Almanac Data: This provides less precise information about the orbits of every satellite in the constellation, aiding the receiver in acquiring and tracking signals from multiple satellites.
• Time Data: precise time information from the GPS atomic clock, crucial for calculating signal travel time and, consequently, the distance to the satellite.

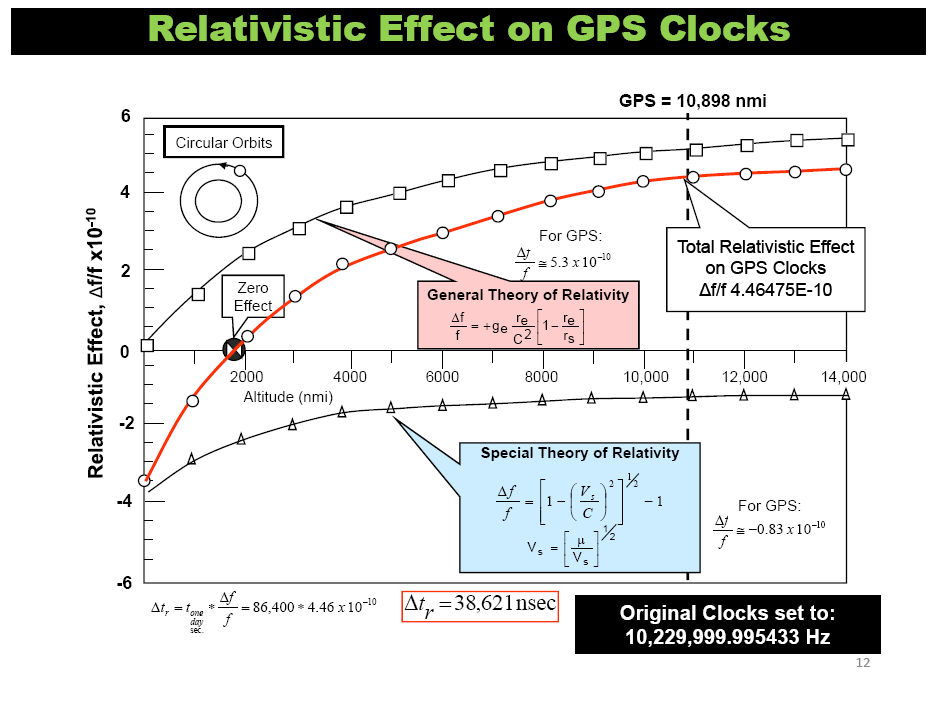
The incredible precision of timing needed for GNSS applications requires consideration of the satellites' high speeds and differing gravitational environment, which introduce relativistic effects which, if unaccounted for, lead to substantial errors in positioning, accumulating to roughly 11 kilometres/day (a ~38 milliseconds/day time difference)[^https://www.gpsworld.com/inside-the-box-gps-and-relativity/]!

Special Relativity

Special relativity predicts that time passes slower for objects in motion relative to a stationary observer. This phenomenon, known as time dilation, affects the atomic clocks onboard GPS satellites. Due to their high orbital speed (~14,000 km/hour), a ~7 microsecond/day delay is introduced. calculated using the following equation derived from special relativity[^ https://www.fourmilab.ch/etexts/einstein/specrel/specrel.pdf]:

\[ \Delta t = t_0 \sqrt{1 - \frac{v^2}{c^2}} \\~\\ \Delta t: \text{ time dilation} \\ t_0: \text{ proper time (time measured by the moving clock)} \\ v: \text{ velocity of the satellite} \\ c: \text{ speed of light} \]

General Relativity

General relativity predicts that time passes slower in stronger gravitational fields. Due to the higher altitude, GPS clocks experience a weaker gravitational field than on Earth's surface, resulting in a ~45 microsecond/day loss.

The equation for gravitational time dilation is[^ https://ia801204.us.archive.org/5/items/the-foundation-of-the-general-theory-of-relativity/The%20Foundation%20of%20the%20General%20Theory%20of%20Relativity.pdf]:

\[ \Delta t = t_0 \sqrt{1 - \frac{2GM}{rc^2}} \\~\\ \Delta t: \text{ time dilation} \\ t_0: \text{ proper time} \\ G: \text{ gravitational constant } (6.674 \times 10^{-11} \text{ m}^3 \text{kg}^{-1} \text{s}^{-2}) \\ M: \text{ mass of the Earth } (5.972 \times 10^{24} \text{ kg}) \\ r: \text{ distance from the centre of the Earth to the satellite} \]

This total discrepancy of ~38 milliseconds/day would result in significant positioning errors, accumulating to roughly 11 kilometres/day[^https://www.gpsworld.com/inside-the-box-gps-and-relativity/]!

The Sagnac Effect

The Sagnac effect causes a difference in the time it takes for light to travel around a closed path in a rotating frame of reference, depending on the direction of travel[^ https://www.gsjournal.net/Science-Journals/Research%20Papers-Relativity%20Theory/Download/8681][^ Relativity in the Global Positioning System by Neil Ashby].

The magnitude of the Sagnac effect can be calculated using the following equation:

\[ \Delta t = \frac{4A\omega}{c^2} \\~\\ \Delta t: \text{ time difference} \\ A: \text{ area enclosed by the light path} \\ \omega: \text{ angular velocity of the rotating frame of reference} \\ c: \text{ speed of light} \]

Other secondary relativistic effects, such as the effects of the Earth's quadrupole moment and the gravitational fields of the Sun and Moon, also contribute to the overall timing corrections required for GPS.

Mitigation

To counteract these relativistic effects, the atomic clocks on GPS satellites are intentionally set to run slightly slower before launch. Furthermore, the satellite clocks are continuously monitored and adjusted as needed by the GPS control segment. This ongoing monitoring ensures the system's long-term accuracy and reliability.