
Physics
Venturing Past the Horizon, A Theoretical Description
What would you see if you fell into a black hole? What might it look like to someone outside? Could you escape once you've fallen though?

Biochemistry
How drugs that replicate the effects of exercise could be a benefit, or detriment to us.

Biotechnology
How Glowee is collaborating with a French municipal government to trial bioluminescent bacteria as a renewable source of public lighting for France

Medicine
Humans have lungs adapted to inhale air and use the oxygen in that air which have served vertebrates since around 400Ma. Using liquid for ventilation in lungs would therefore seem absurd. Indeed, in normal healthy lungs, liquid breathing as one would expect worsens gas exchange. However, in cases of

What would you see if you fell into a black hole? What might it look like to someone outside? Could you escape once you've fallen though?

How drugs that replicate the effects of exercise could be a benefit, or detriment to us.

How Glowee is collaborating with a French municipal government to trial bioluminescent bacteria as a renewable source of public lighting for France
Discover the latest developments in Science, Technology, Engineering and Maths for all levels from the boys of Eton College.

The STEM Committee's science exhibition captivated the audience with a whirlwind of hands-on science and mind-bending experiments. From exploring the hidden world of pixels to dissecting a sheep’s brain and testing memory, the night was filled with “wow” moments. From an intense battle between an at

Project CETI (Cetacean Translation Initiative), led by biologist David Gruber, is getting ever so close to bridging the gap between sperm whale ‘clicks’ and human words. Breakthroughs in artificial intelligence, especially in the use of machine learning techniques, have allowed algorithms to identif

Antibiotic resistance, driven by evolution, has become a critical global threat. The misuse of antibiotics in healthcare and agriculture accelerates the rise of resistant bacteria like MRSA. These "superbugs" lead to millions of infections and thousands of deaths each year.

A hot air balloon uses a gas flame to heat the air it contains to a temperature required to enable it to hover at a small distance above ground level. The mass of the balloon, ropes, basket, and riders is 240 kg and the volume of the balloon is 1100 m³. The temperature of the surrounding air is 15°C

Nanotechnology is revolutionizing neurological medicine by enabling precise drug delivery and treatments. Techniques like PLGA and Cadmium Selenide nanoparticles bypass the blood-brain barrier, targeting conditions such as Alzheimer’s disease. With methods like lithography and vacuum deposition, the

A drunk performs a random walk along a street. At one end of the street is a river, and at the other end is a police station. If he gets to either of these ends, he remains there. He starts n steps from the river, and there are N total steps between the river and the police station. What is the prob

Neutron stars are born from the explosive deaths of massive stars, known as Type II supernovae. These dense celestial objects, only about 20 kilometers in diameter, possess extreme characteristics such as rapid spin rates and intense magnetic fields. The formation process involves complex nuclear re

NFTs, often misunderstood as mere digital images, redefine ownership by leveraging blockchain technology for transparency and easy trade. Unlike cryptocurrencies, each NFT is unique, making it valuable for verifying ownership and tracking provenance. Despite their benefits, NFTs also pose risks such

Smartphone cameras embody several functionalities akin to traditional cameras but offer the added convenience of compactness. Moreover, they leverage digital techniques, including AI-powered editing, to augment image quality and enhance user experience.
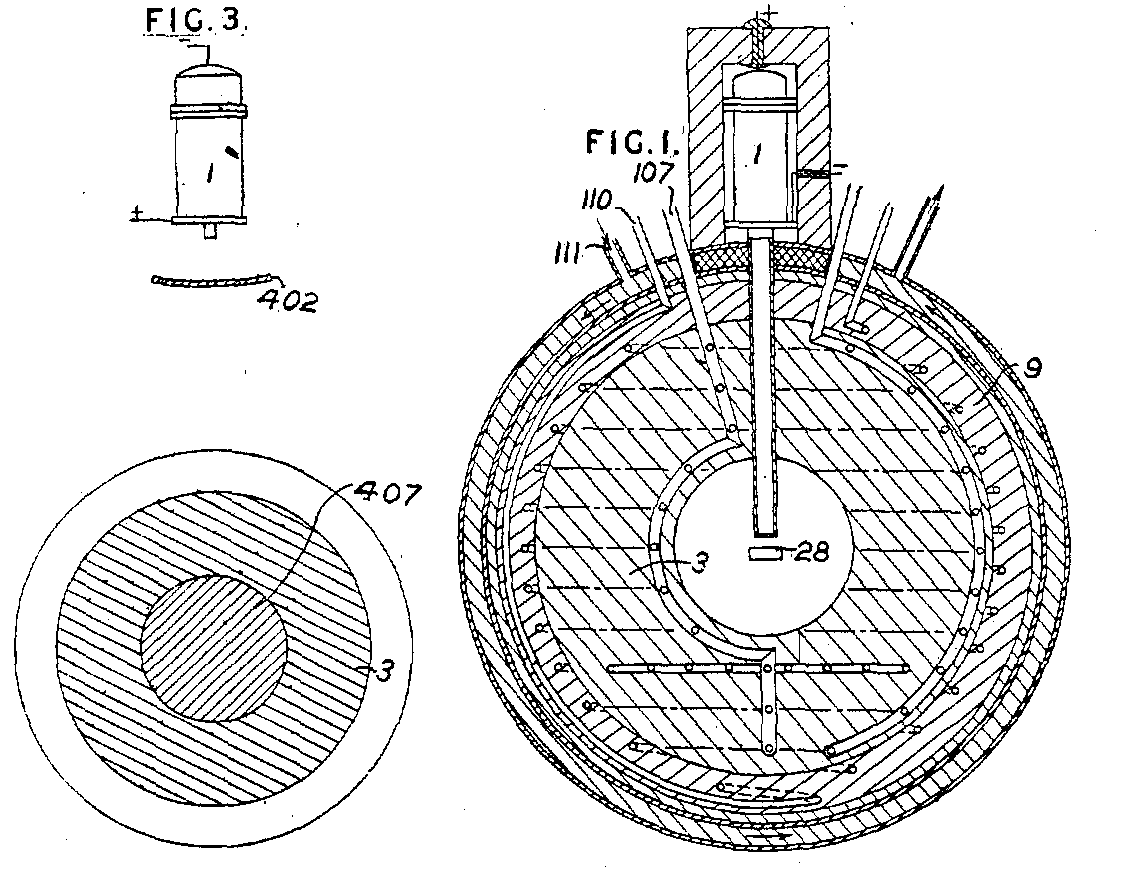
While citizens of New York sat down for supper, an American bomber dubbed the Enola Gay revealed a breakthrough: the Little Boy, the world’s first and most devastating atomic bomb. This bomb, rooted in a British patent by physicist L. Szilard, marked the culmination of six years of scientific innova

Radiation Pressure is a force that is exerted upon a surface due to the exchange of momentum between the object and the electromagnetic field. This includes electromagnetic radiation of any wavelength, including visible light, radio waves and gamma rays.

CT scans are a vital medical imaging technique for diagnosing, treating, and preventing diseases by providing detailed cross-sectional images of the body. By converting X-ray attenuation data into a sinogram, CT scans visualize internal structures with high precision. Advances like helical scanning