
Biology
From Commensal to Pathogen: The Mechanisms Behind Bacteria
Explore the roles of host susceptibility, virulence factors, genetic adaptation, and environmental triggers in the sudden change of the bacteria from commensal to virulent

Chemistry
An introduction to the complicated life and contrasting legacy of the man behind the prizes.

Biochemistry
When people think of genetic mutations, they would normally think that they're caused by radiation, carcinogens or copying errors when replicating DNA. However, recent studies show quantum tunnelling also has an effect here.

Physics
An introduction to the incredible materials which make modern aviation possible.

Have you ever wondered how your brain really functions—your thoughts, your memories and how we, humble humans, can achieve the feats we do? Well, wonder no longer, as this article will unveil how memories and emotions are created through phenomena such as active potentials and more

Hydrogen powered cars present a sustainable transport alternative to electric cars. However, there are many questions to be answered: are they more environmentally friendly? Are they economically viable?

Imagine being told that the same useless numbers which you consistently label as redundant in the real world are in fact key to keeping your data safe from prying eyes. Every time someone sends a message, numbers keep your information safe and hidden so only the receiver can see it.

The Rubik’s Cube is far more than a colourful toy—it is a mathematical marvel that embodies the beauty of symmetry, structure, and problem-solving.

The natural world is filled with complex and unpredictable phenomena, from weather patterns to the dynamics of ecosystems and the stock market. At first glance, these systems may seem entirely random, yet there are often underlying deterministic laws governed by mathematics.

Take a deep dive into the growing role of Nanotechnology in Medicine, and learn about the complex technologies being developed.
Discover the latest developments in Science, Technology, Engineering and Maths for all levels from the boys of Eton College.

Fast cars, cheese, and cutting-edge design. The Eton College 2025 Design trip to Italy blended roaring engines with rich tradition. From Ferrari and Ducati to Parmigiano Reggiano, students explored engineering, culture, and craftsmanship at its finest.

Andrew Jia In the modern world, vacuum tubes see use in a very limited range of applications and may be regarded as obsolete technology. However, they have played an important role in computing history. The first vacuum tube device was conceived in 1904 by John Fleming and took the form

F1 is more than just a race - it’s a showcase of engineering brilliance. With turbocharged V6s, energy recovery systems, and state-of-the-art aerodynamics, teams battle for every fraction of a second. Explore the tech behind the world's fastest sport and how it fuels innovation beyond the track.
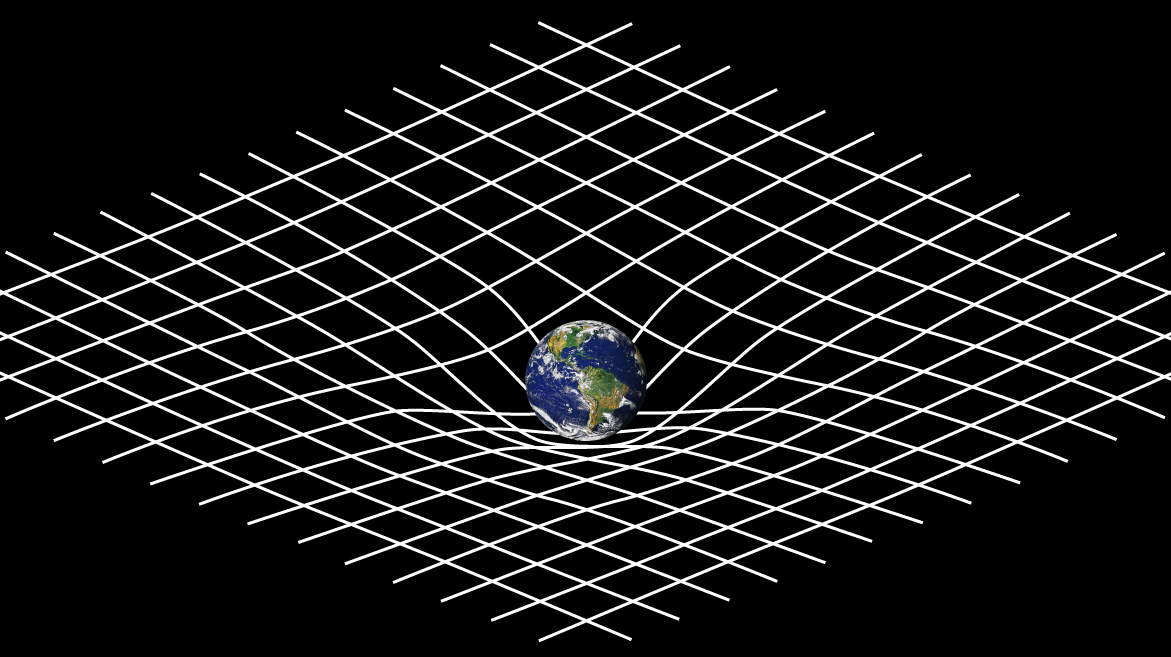
Einstein's Field Equations are among the most famous equations in all of physics, and yet what do they describe, and how do they work?
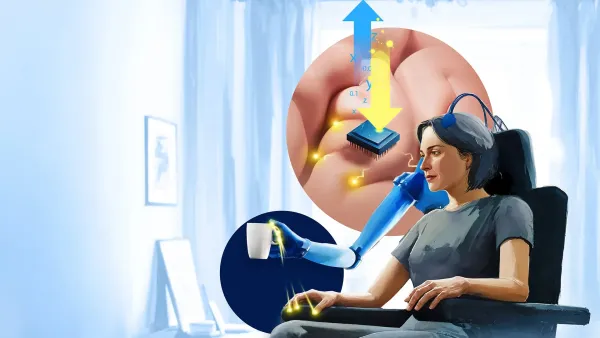
Discover how a group of researchers in Sweden are pioneering the world's first bionic limb that can sense touch

The End of British Science Week A Note From AZB British Science Week: Celebrating Discovery, Innovation, and Future Scientists Every year, British Science Week (this year running from 7th – 16th March… yes, slightly longer than a week…) brings together schools, communities, and scientists across the UK to celebrate the incredible

Can carbon capture save the planet, or is it just another costly distraction? Methods like post-combustion capture and direct air capture aim to reduce atmospheric CO2 levels. However, concerns about cost, energy use, and effectiveness raise questions about its role in fighting climate change.

You're receiving this email because you are affiliated with Eton College. (Best viewed on the website) We as EtonSTEM are delighted to announce that it is the start of British Science Week, which is a ten-day celebration for anything and everything STEM. Throughout the week, we’ll be

Reminder of This Year's Theme: Adapt and Change We are midway through British Science Week, so it's a great time to remind you to observe how STEM shapes the world around us. With the rapid development of technology, it is important to know how to adapt

Reminder of This Year's Theme: Adapt and Change We are midway through British Science Week, so it's a great time to remind you to observe how STEM shapes the world around us. With the rapid development of technology, it is important to know how to adapt
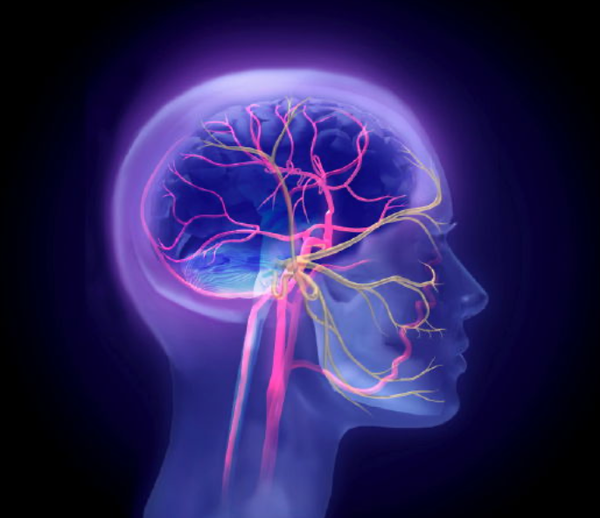
You're receiving this email because you are affiliated with Eton College. (Best viewed on the website) Welcome to Day 2 of British Science Week, and today's main focus is biology. We will observe how biology shapes the world around us, and what crazy things scientists are
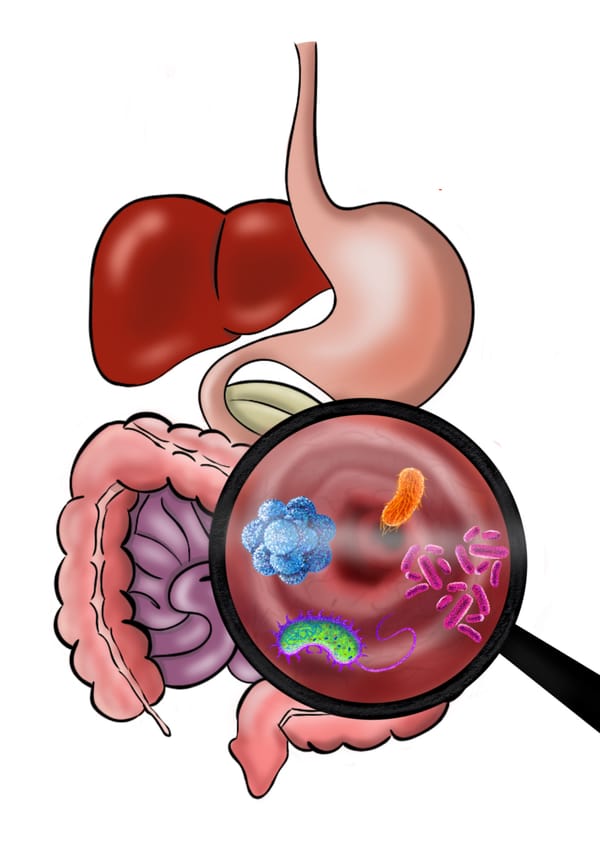
Take a brief dive into the microbial populations within our bodies several orders of magnitude larger than that of humans on Earth, and the critical functions these microbes play in our health